Purely Functional Data Structures & Algorithms : Red-Black Trees in Qi

Update 2011/06/28 : Source has been modified to compile with Shen

This is the first in a series of posts that will demonstrate the implementation of many well-known(and less known) data structures and algorithms using a purely functional approach.
We will use Qi as our implementation language for a number of reasons :

    It’s a Lisp : macros, EVAL, hash-tables, property-lists, meta-programming etc.
    Pattern matching.
    Optional static type checking.
    A Turing-complete type system !

In this first post we look at an implementation of the well-known Red-Black tree abstract data type in Qi.

A red–black tree is a type of self-balancing binary search tree, a data structure used in computer science, typically to implement associative arrays. The original structure was invented in 1972 by Rudolf Bayer and named “symmetric binary B-tree,” but acquired its modern name in a paper in 1978 by Leonidas J. Guibas and Robert Sedgewick. It is complex, but has good worst-case running time for its operations and is efficient in practice: it can search, insert, and delete in O(log n) time, where n is total number of elements in the tree. Put very simply, a red–black tree is a binary search tree that inserts and removes intelligently, to ensure the tree is reasonably balanced.

Our implementation comes in at 57 lines of code (with the balance function at only 7 lines) 

(tc +)
(datatype tree-node
    Key : number; Val : B;
    ======================
    [Key Val] : tree-node;)
(datatype color
    if (element? Color [red black])
    _______________________________
    Color : color;)
(datatype tree
    if (empty? Tree)
    ________________
    Tree : tree;
    Color : color; LTree : tree; TreeNode : tree-node; RTree : tree;
    ================================================================
    [Color LTree TreeNode RTree] : tree;)
(define node-key
    {tree-node --> number}
    [Key Val] -> Key)
(define make-tree-black
    {tree --> tree}
    [Color A X B] -> [black A X B])
(define member
    {tree-node --> tree --> boolean}
    X NIL -> false
    X [Color A Y B] -> (if (< (node-key X) (node-key Y))
         (member X A)
         (if (< (node-key Y) (node-key X))
             (member X B)
             true)))
(define balance
    {tree --> tree}
    [black [red [red A X B] Y C] Z D] -> [red [black A X B] Y [black C Z D]]
    [black [red A X [red B Y C]] Z D] -> [red [black A X B] Y [black C Z D]]
    [black A X [red [red B Y C] Z D]] -> [red [black A X B] Y [black C Z D]]
    [black A X [red B Y [red C Z D]]] -> [red [black A X B] Y [black C Z D]]
    S -> S)
(define insert-
    {tree-node --> tree --> tree}
    X [] -> [red [] X []]
    X [Color A Y B] -> (if (< (node-key X) (node-key Y))
                           (balance [Color (insert- X A) Y B])
                           (if (< (node-key Y) (node-key X))
                               (balance [Color A Y (insert- X B)])
                               [Color A Y B])))
(define insert
  {tree-node --> tree --> tree}
  X S -> (make-tree-black (insert- X S)))

This is a reasonably performant implementation (we haven’t even tried to optimize it yet).

(19-) (run-tests NIL)
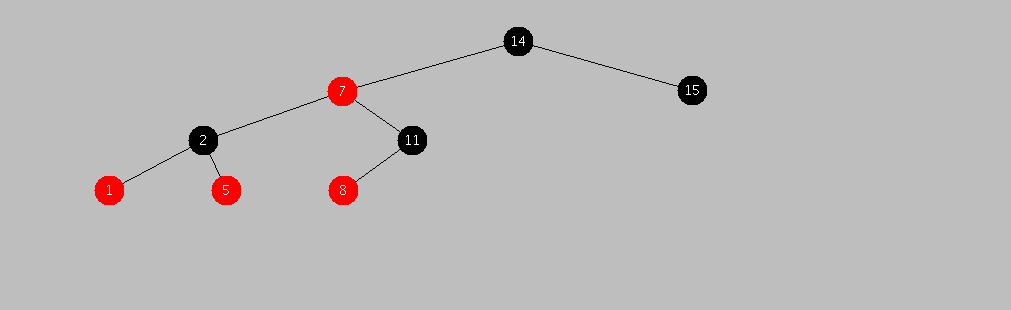
tree: [black
       [red [black [red [] [1 1] []] [2 2] [red [] [5 5] []]] [7 7]
        [black [red [] [8 8] []] [11 11] []]]
       [14 14] [black [] [15 15] []]]
12 is a member ? false
8 is a member ? true
Creating tree with 100000 elements ...
Evaluation took:
  0.578 seconds of real time
  0.562833 seconds of total run time (0.491572 user, 0.071261 system)
  [ Run times consist of 0.160 seconds GC time, and 0.403 seconds non-GC time. ]
  97.40% CPU
  1,210,617,335 processor cycles
  168,551,696 bytes consed
Performing lookups in tree with 100000 elements ...
666 in tree ? true
Evaluation took:
  0.000 seconds of real time
  0.000044 seconds of total run time (0.000035 user, 0.000009 system)
  0.00% CPU
  86,110 processor cycles
  0 bytes consed
-1 in tree ?
Evaluation took:
  0.000 seconds of real time
  0.000024 seconds of total run time (0.000021 user, 0.000003 system)
  100.00% CPU
  46,368 processor cycles
  0 bytes consed

A comparable implementation in Java/C++ will usually run a few hundred lines of code.
All Qi code in this post is here.